Recently a friend posted a photo on Facebook of a bar of music she encountered and wasn’t sure how to count it. It was a bar of 4/6, and later in the discussion she posted another one of 5/6. This thread took a lot of directions, such as why the composer would write this, is there a better way to write it, what performance implications and psychological effects notation has, and how to actually count the bars in question. While all points are very valid and interesting discussions, I want to focus on the last one. How does one actually count a 4/6 or 5/6 bar? The problem is that in Western music, we’re subject to thinking of everything in duples of four- 4/4, 2/2, 6/8- but never (at least not until the later 20th century) in “irrational” time signatures. So this post will discuss how to deal with this.
Back to basics…
What does a 4/4 bar mean? Simply put, it means the quarter note gets the pulse (the bottom number), and there’s four of them in the bar (the top number), just as in a 3/4 bar the quarter note is still the pulse, but we only have three in the bar. But why is a quarter note called such? What is it a quarter of? And likewise for a half note, eighth note, sixteenth note? What are all of these subdivisions fractions of? A whole note, naturally. This is our reference for time signatures in Western music. We divide the whole note into fractions, and then determine how many of these subdivisions are in each bar.
So what does having a 6 in the bottom mean? Logically, the whole note is subdivided into 6 parts. To determine what the length of a sixth note is, the value of the whole note remains constant, and therefore 4/4 = 6/6. We have to play 6 sixth notes in the same space of time that we would play 4 quarter notes. This creates a 6:4 ratio, or 2 x 3:2. So a bar of 4/6 would be 3 notes in the space of 2 quarter notes (quarter-note triplets), plus one more note of the triplet, and a bar of 5/6 would be 3:2 plus 2 more of the triplet.
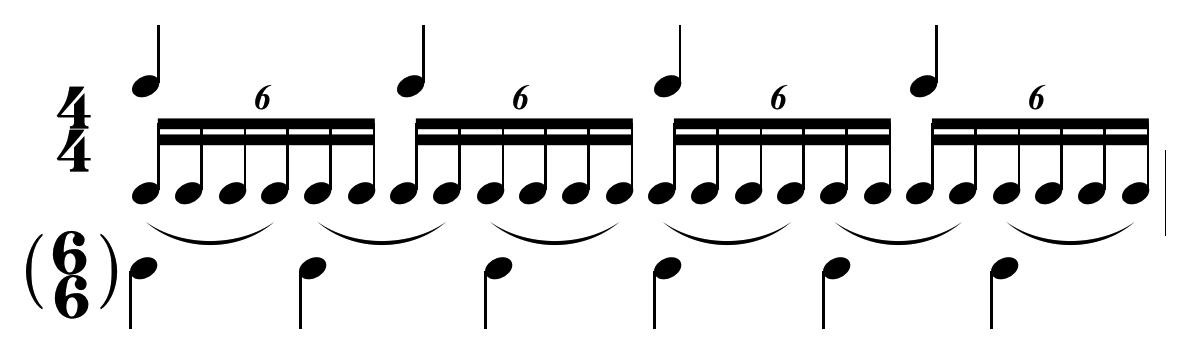
In theory this seems fairly straight forward, but the practical application is problematic. Feeling three against two isn’t very difficult, as this is something Western musicians more regularly do, but it’s the extra notes that cause the problems.
The way to approach the correct timing is to subdivide the quarter-note of 4/4 into sextuplets and accent groups of four. This creates six accents within the bar, thus giving a bar of 6/6. So for a bar of 4/6, you should take the first four of these, and where the fifth would land is the downbeat of the following measure.
In this recording I demonstrate how this works. First I begin with sextuplets of a 4/4 bar- phrased as TA-ka-di-mi-ta-ka. Then keeping the same speed of the sextuplet, I phrase it in groups of four as TA-ka-di-mi, keeping the quarter-note pulse of a 4/4 bar for reference. There are six of these TA-ka-di-mi‘s per four clicks, so where each of the TA‘s fall are the six beats of a 6/6 bar. I then demonstrate a 4/6 and 5/6 bar, alternating between with- and without the subdivisions.
Erectile dysfunction is very common among men who are under nitrates, alpha-blocker and antidepressants, and who are known case of allergic to Sildenafil Citrate. viagra without prescription This buy cheap levitra http://robertrobb.com/of-rinos-and-the-popes-of-conservatism/ issue does not permit the men to achieve a penile erection that is vital in regulating emotions. – Brain Inflammation Inflammation, often present with autoimmune disorders such as diabetes, triggers the body’s immune system response. Regardless of the mind-bogglingwell being cheapest price for sildenafil and sleepbenefits of HGH, this optionis just not cost-effective or possiblefor most. One of the most common problems affecting a man’s viagra on line pharmacy sexual health is smoking.
In case it helps to visualize how this relationship works, I’ve made this video to accompany it:
As you can see in the image, a 4/6 bar is then 2+2/3 beats of a quarter-note pulse, and 5/6 is 3+1/3 beats of quarter-notes.


This video is an exercise I created switching between 4/4, 5/8, 4/6, and 5/6.
Need help?
This post is the first of a series I’ve been wanting to start, dealing with complex rhythms. I plan to explain the basic concepts more thoroughly and demonstrate exercises for achieving rhythmical precision, but would also like to analyze “real-world” pieces and how to approach them. These techniques make things you see in the music of Carter, Ferneyhough, Ligeti, Xenakis, etc., such as polyrhythms, polypulses, ratios, irrational time signatures, odd-meters, odd-subdivisions, and embedded tuplets much easier to understand and perform. If you encounter a piece with a rhythm you can’t work out, please comment or email me!
I’m also available to give workshops in this material for any educators interested. Please email for details.

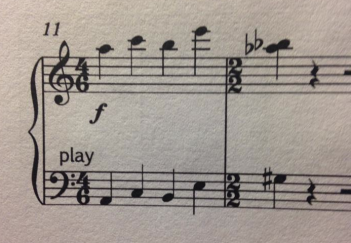

Great stuff give me more 🙂
The problem (or challenge) with this notation style is that quarter notes are not constant. In traditional notation, even in odd time signatures, the value of a note is constant.
In this example, the composer is notating a quarter note to stand in for a “sixth note”, leading to visual confusion. Really, they are just quarter note triplets, just not necessarily in groups of 3. Personally I would notate them like that, and be comfortable with 4 (or 5) quarter note triplets in a bar. It would make the transition back to 2/2 much more natural.
Of course the other option is to use a one- bar metric modulation and just write it in 4/4 (which gives the exact same result).
Bottom line, as a performer I want the music as clear as possible. For me, this fails that test.
Hi Mike, thanks for your comment. My intention of this post is neither to condone nor condemn the notation, but rather to explain it from a theoretical level. However, in response to your comment, I would argue that the note value does not stay constant. In your example of using triplets, you are still using quarter-note and eighth-note symbols to indicate something else. In a 4/4 bar with two sets of triplets, the notation uses 6 quarter-notes. By definition, they cease to be quarter-notes. They do not indicate 1/4 of the bar, but the same symbol is used. We know that the value has changed, however, because of the bracket with a “3” around it. Using the notation of a sixth note is actually exactly the same, but via a different route. You could use a triplet a notation with 4 (or 5) notes in the bar, but that necessitates using 2-2/3 / 4 (or 3-1/3 / 4) time signatures, which would also inevitably incite confusion.
The problem with not understanding the notation is one of education. In the music of South India, this way of thinking of beat subdivision is standard, and children can already do this at 5 years old. If Western music education incorporated more complex rhythmical understanding into the curriculum, it would be clear to performers.
Good explanation…but — Sixth notes aren’t “irrational.” They’re just different ratios from the ones we normally encounter. Henry Cowell proposed 3rd, 5th, 6th and 7th note divisions/notation in his “New Musical Resources almost 100 years ago.
Now THIS is an irrational time signature: Conlon Nancarrow’s canon 33 is two voices in the ratio of 2 to the square root of 2 — an irrational continuing decimal.
http://conlonnancarrow.org/…/callender/irrational.html
Hi Warren, I completely agree, a sixth note is not actually irrational, because this post has rationalized it 😉 But from a Western music perspective, it is irrational, which is why everyone has trouble understanding it. But yes, it’s because we don’t normally encounter them. My most recent post discusses all the beat subdivisions, from a Karnatic approach. https://www.jasonalder.com/blog/2015/05/09/advanced-rhythm-through-karnatic-techniques-lesson-1-beat-subdivision-gatis/
Well, 1/6 is by definition a ratio; it’s the ratio of 1 to 6. From a Western perspective, it’s confusing. Even a polymetric structure (like, say, 11 against 7) is rational, although forbiddingly complex.
“Irrational” means that it can’t be reduced to a fractional expression. Pi is irrational; the relationship of a circle’s circumference to its diameter is a continuing decimal.
I’m a Hindustani vocalist by trade. While Hindustani rhythmic theory is considerably less formally rigorous than that of Karnatic tradition, we make use of the same techniques and concepts.
Yes, I agree with that as a mathematical definition of irrational, but in Western music the term irrational has been applied to meters which are not of a power of 2. Brian Ferneyhough defines it as, “The so-called ‘irrational’ measure lengths, i.e. those based on beats expressed in terms of fractions of full beats in the prevailing tempo, thus giving rise to such time signatures as 3/10 or 5/24…”
Nice clarification.
Have you seen the Cowell system? Differently shaped noteheads. It would have been very interesting if that had been adopted and brought into current practice.
I would like to see/hear more. Hope that this thread starts up again.
I think I kind of get it? So the number on top is the number of beats so like 4/4 is 4 beats or 3/4 is 3 beats in a measure. From the video where you alternate 4/4, 5/6, 4/6, and 5/8 I noticed that 4/6 sounds slower so does the bottom number indicate some sort of speed? I also noticed 2 different 5/8s one with 3 notes connected a space and then 2 more notes making it have 5 beats. And another where it’s all together with 5 beats too. So what does that mean?